Implied odds não são difíceis de entender, mas muitos jogadores as aplicam erroneamente dentro das mesas. Isso leva a erros desnecessários, que poderiam ser evitados, que acabam custando muito caro, como tentar acertar um draw que não vale a pena.
Para ajudá-lo a evitar tais erros, sistematizamos ideias ao redor do conceito de implied odds para ajudar a moldar sua tática dentro das mesas. Neste artigo nós vamos ver:
- O que são implied odds?
- Como as implied odds funcionam?
- Dois exemplos de mãos que mostram o uso das implied odds (incluindo um spot que pode te surpreender)
Vamos começar!
O que são implied odds?
Implied odds é a quantidade de dinheiro que você espera ganhar em apostas futuras caso você acerte um de seus outs. Esse conceito, junto com pot odds, normalmente é usado para te ajudar a saber quando vale a pena dar call em um aposta esperando um draw.
LEIA TAMBÉM: Entenda o que são outs e pot odds no poker
Se você espera ganhar mais dinheiro com seu oponente depois de acertar seu draw, então você tem boas implied odds. Mas se você não conseguir mais dinheiro do seu oponente nas apostas futuras, então você tem pouca ou nenhuma implied odds.
O que você pode calcular, no entanto, é o valor mínimo que você precisaria ganhar nas apostas futuras para justificar um call que não perca dinheiro. Isso é o que abordaremos na próxima seção.
Como que as implied odds funcionam?
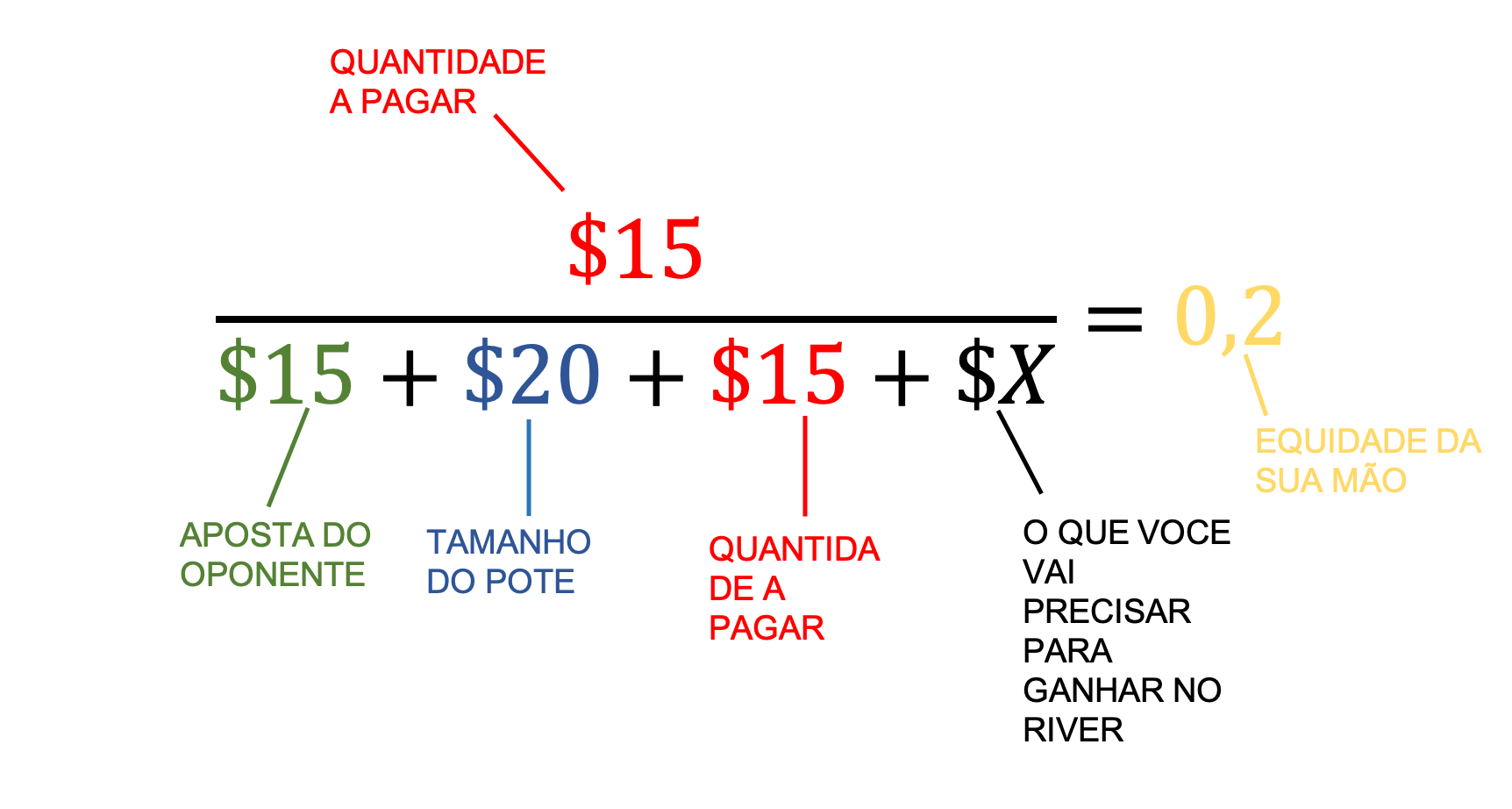
Imagine que você está jogando cash game $1/$2 e você tem K♥️ Q♥️ no turn e está em posição. O bordo é A♥️ 6♦️ 2♠️ 9♥️ – te dando o flush draw nuts – e seu oponente aposta $15 em um pote $20.
Uma rápida conta de pot odds ($15 para pagar/($15 aposta + $20 pote + $15 para dar call) mostra que você precisa ter mais de 30% de equidade para dar um call rentável. Como você só tem ~20% de chances de bater um flush com uma carta para virar, você deveria foldar essa mão caso nenhuma outra ação for levada em consideração.
É aqui que entram as implied odds. Aqui está a fórmula para descobrir quanto dinheiro você precisa ganhar no river para justificar um call no turn:
Se você notar ela é muito similar a formula de pot odds. A única diferença é a adição do “X” no denominador e sua equidade depois do sinal de igualdade.
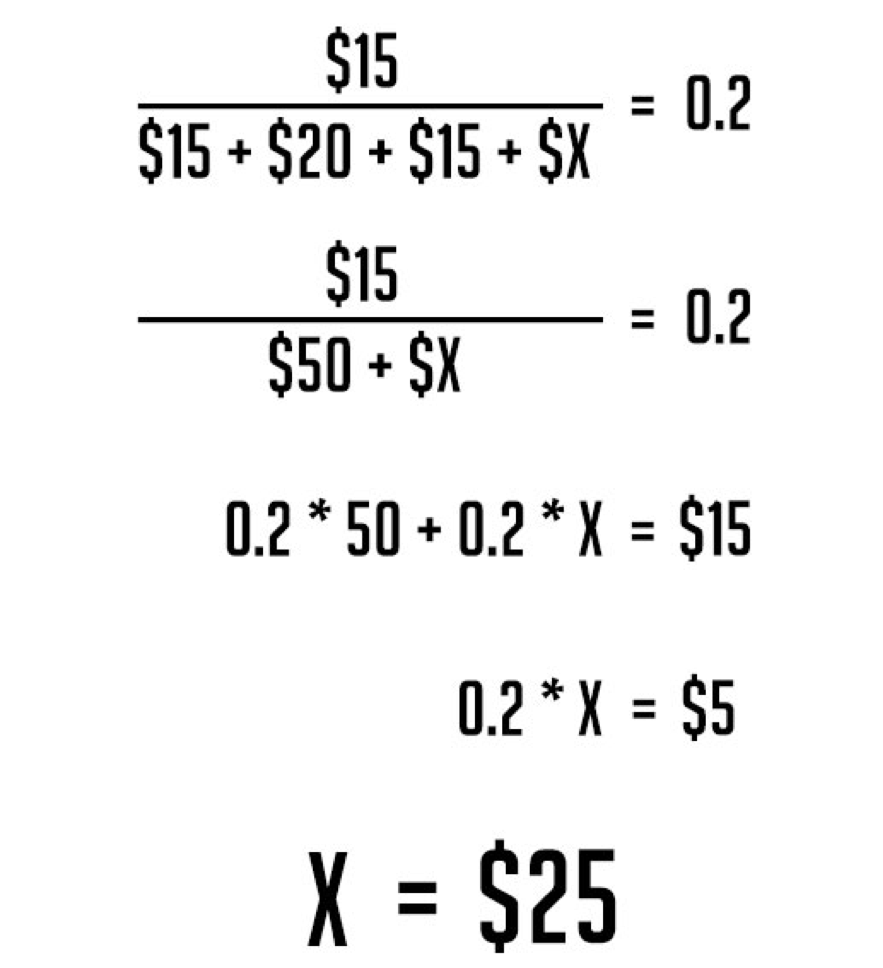
Agora, vamos resolver o ‘X’:
Isso significa, que se você atingir o flush no river com K♥️ Q♥️, você vai precisar ganhar mais do que $25 para que pagar o turn seja rentável. Como o pote já é de $50, você só teria que extrair, na média, metade do pote.
Esse resultado parece bastante viável, especialmente com o potencial de ganhar um grande pote em situações de flush-vs-flush. Então, você deve dar call no turn nessa mão.
Exemplos de Implied odds
Vamos percorrer alguns exemplos para encaixar este conceito em sua cabeça. Prepare-se, isso pode ficar um pouco mais desafiador.
Big Blind vs. Button (single raised pot as the preflop caller)
Exemplo 1: Big Blind vs. Botão
Suponha que você esteja fora de posição (OOP) no BB e o defensor da mão tem J♦7♦. Você acabou de dar call em um c-bet no flop. No turn, o bordo é K♦ T♦ 3♠ 2♥, e você encara uma aposta de $50 em um pote de $67 do jogador que esta no botão, que tem $117 para trás (você cobre).
Suas pot odds são: $50/$167 = 0,3= 30% de equidade para realizar um call lucrativo.
É assim que sua equidade se parece (destacada no quadrado roxo) contra um segundo barril bem balanceado:
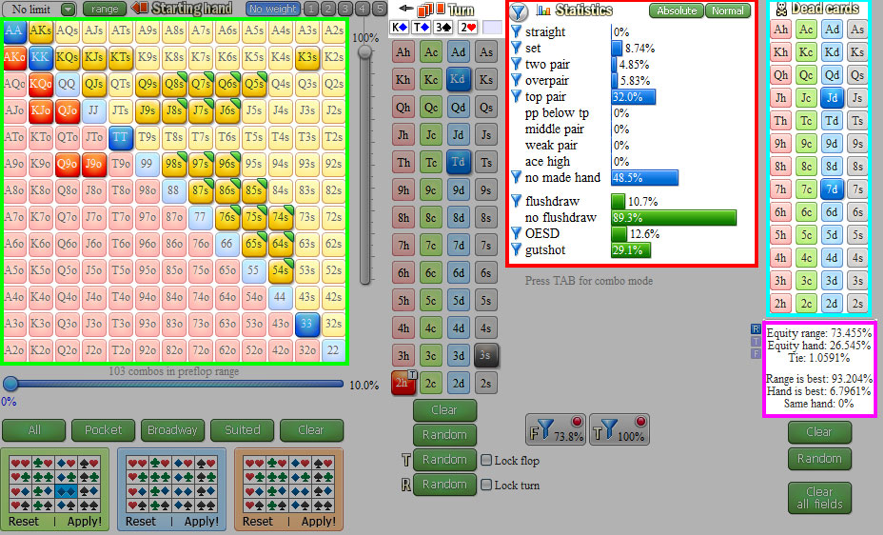
Você pode ver que não temos equidade suficiente para pagar se levarmos em consideração apenas as probabilidades do pote, já que temos apenas 26,5% de equidade. Mas esta é uma avaliação incompleta da situação – não levamos em consideração o que acontecerá no river.
Vamos fazer o flush no river 19.6% do tempo – vamos arredondar para 20% para facilitar o cálculo. Além disso, para simplificar, vamos supor que toda vez que fizermos o flush no river, ganhamos o pote (na verdade teríamos a melhor mão ~ 96% do tempo).
Agora, vamos usar a fórmula de antes para calcular quanto dinheiro precisamos ganhar no river para empatar o lucro do call:
50/(50 + 50 + 67 + X) = 0.2
50/(167 + X) = 0.2
50 = 0.2 * 167 + 0.2 * X
50 = 33.4 + 0.2 * X
0.2 * X = 16.6
X = 16.6/0.2
X = $83
Precisamos ganhar $ 83 no botão assim que acertarmos. O pote será de $ 167 no river, o que significa que temos que extrair uma aposta de meio pote para empatar – e lembre-se, o botão só tem $ 117 para trás.
Já que o botão não vai atingir 100% do tempo no river, especialmente quando o flush draw atinge, você precisa fazer uma das seguintes estratégias para extrair o valor necessário:
- Donk-bet. Se escolhermos esta opção, a reação do nosso oponente deve nos custar $ 83 em média. Por exemplo, se apostarmos all-in por $ 117, o botão teria que pagar pelo menos 70% do tempo.
- Check-call (ou check-raise se ele aposta all-in). Novamente, isso precisaria nos custar US $ 83 em média. Por exemplo, ele precisaria empurrar $ 117 pelo menos 70% do tempo, a fim de empatar o nosso call do turn.
Esses resultados são possíveis, mas não é muito provável que eles demonstrem o quanto precisamos deles. Ao contrário do exemplo do K♥ Q♥ , não teremos nuts quando batemos, estamos fora de posição e não há muito para ganhar. Todas essas razões tornam a extração do valor necessário no river muito mais difícil.
Você pode ver porquê, mesmo com a adição de implied odds em nossa avaliação, ainda não podemos pagar lucrativamente com um draw fraco. Nossa avaliação, no entanto, mostra que esse call não é tão ruim quanto parecia anteriormente.
[learn_more caption=”Nota” state=”open”] O cálculo aqui é simplificado para excluir alguns fatores que, mesmo quando incluídos, têm um impacto insignificante no resultado. Esses fatores incluem acertar um J ou 7 no river e ganhar o pote quando a ação é controlada, quando ficamos trombamos um flush maior e perdemos muito, e quando ficamos com um flush maior e ganhamos muito.[/learn_more]
Button vs. Big Blind
Exemplo 2: Botão vs. Big Blind
As implied odds não são usadas apenas quando se enfrenta apostas com draws. Eles são importantes quando você é o agressor da mão. Considere a seguinte situação:
Você subiu primeiro do botão e foi pago pelo BB. O flop é ♣ 8♦ 5♥.
Você está tentando construir sua estratégia de c-bet e para isso é necessário considerar suas implied odds. Para mostrar isso, vamos considerar duas opções de mãos: J♥ 9♥ e A♦ J♠.
Primeiro J9hh. Esta é uma mão (top pair com kicker médio) que consegue extrair 2 streets de valor, então a questão é como extrair o maior valor: devemos apostar flop, betar turn e checkar river ou betar no flop, checkar no turn e betar no river, ou checkar no flop, betar no turn e betar no river?
Vamos considerar os cenários possíveis quando melhoramos para dois pares em um turn 9 – uma estratégia chave no turn quando se trata dessa mão:
Cenário 1: Você c-beta e é pago. O turn é um 9. Você agora é percebido como tendo um range mais forte, dado que QT, T7s e 76s foram completados. Isso significa que você obterá menos valor de seus dois pares e sofrerá de implied odds reversas quando seu oponente tiver QT.
Cenário 2: Você c-beta e sofre um raise. Você paga e o turn é um 9 novamente. O seu oponente irá apostar com muita frequência nesta carta, já que seu range melhorou drasticamente como resultado de da conexão com seus draws como 76, QT, T7. Você é forçado a dar call e já sabe que não vai ser divertido daqui para frente.
Cenário 3: Você da check e o turn é 9. Seu oponente agora tem uma tonelada de possíveis mãos blefáveis, como AT, KT, T6s, T4s, T3s, T2s, KQ, Q7s, Q6s, Q4s, Q3s, Q2s, etc. Ele estará colocando muita pressão em você com estas mãos desde que seu QT, T7s e 76 terminaram, e você estará lá com uma mão muito forte para pagar.
Você pode ver nesses cenários que é melhor dar check nessa mão. Ele joga muito bem no turn, melhorando a carta que será mais ferozmente atacada pelo seu oponente.
Em seguida, vamos pegar o AJ. Com esta mão, haverá alguns runouts onde você ganha 3 apostas de valor e alguns onde você só recebe 2. Então, nós diremos que esta mão vale 2.5 apostas de valor. Como Podemos extrair o máximo de valor?
Mais uma vez, vamos nos concentrar no turn que nos dá dois pares – um ás – já que esta é uma estratégia chave no turn para esta mão:
Cenário 1: Você c-beta e é pago. O turn é um ás. Isso melhora seu range mais do que o big blind, o que significa que ele ficará um pouco mais relutante em pagar um segundo barril com com mãos como 8x e 5x. Independentemente disso, você tem uma mão muito forte sem que o draw esteja completo, e você quase sempre será capaz dar um terceiro tiro no river por valor.
Cenário 2: Você c-beta e encara um raise. Você paga e no turn vem um ás. Esta carta melhora o seu range mais do que o big blind, o que significa que ele será um pouco mais cauteloso em blefar (em geral). Ainda assim, sua mão agora melhora para superar alguns de seus valores e nenhum sorteio foi concluído, o que significa que você tem um call fácil.
Cenário 3: Você dá mesa também e o turn é o ás. Esta carta melhora seu range dramaticamente e seu oponente irá dar mesa com uma frequência muito alta. Consequentemente, você obterá valor limitado de suas mãos blefando.
Você pode ver claramente porque é que o c-bet com AJ é uma obrigação nesta situação. Todos os cenários incentivam a colocação de dinheiro no pote imediatamente.
Conclusão
As chances implícitas não são importantes apenas quando você está defendendo, também é crucial quando estamos atacando. Eles ajudam a moldar seus ranges de defesa e ataque, e podem ter um grande impacto na sua taxa de vitórias se você usá-los corretamente. Uma compreensão adequada das implied odds ajudará você a gerar situações muito fáceis e lucrativas com mais frequência.
Isso é tudo por hoje! Espero que você tenha gostado deste artigo e aprendido algo com ele. Como de costume, se você tiver alguma dúvida ou comentário, não hesite em usar a seção de comentários abaixo.
E boa sorte, grinders!
Artigo escrito por Dan B. para a Upswing, em 13 de Novembro de 2018.
Traduzido e adaptado por Luigi Soncin.